KMP

KMP 算法可以用 O(n)O(n) 的复杂度在一个字符串中匹配子串。要理解 KMP 算法的原理，需要首先用暴力算法写一个匹配字符串的方法，如下:

1
2
3
4
5
6
7
8
9
10
11
12
// s: 母串, p: 模板串
for (int i = 0; i < strlen(s); i++) {
    bool matched = true;
    for (int j = 0; j < strlen(p); j++) {
        if (s[i+j] != p[j]) {
            matched = false;
            break;
        }
    }
    
    if (matched) foo();
}

这种做法不好的地方在于它没有充分利用已知条件，做出很多重复的判断，而 KMP 算法就是利用模板串中的特点来减少重复判断。

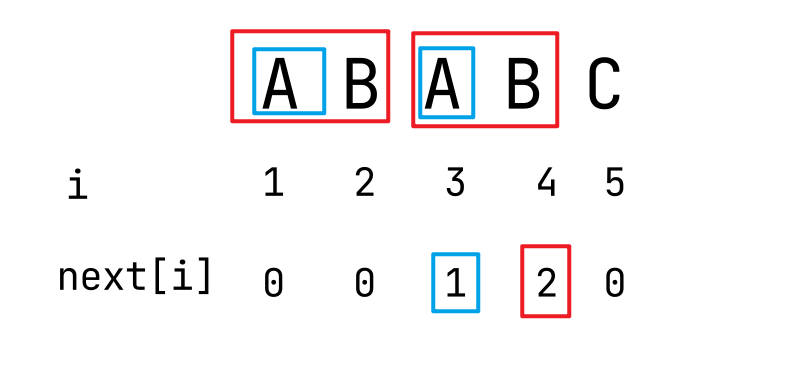
原理是将模板串中任意一个地方的 s[i] 都预先找到一个数值 n = next[i]，意思是到 i 位置的字符串为止相同前缀后缀的长度，即 s[~n] == s[i-n~i]，如下图所示：

匹配

先跳过如何构造 next 数组，我们来关注如何匹配子串。

因为对于子串 pp 中每一个 j 都有一个 next[j] 前面的部分相等，所以当一位匹配失败时就可以退回到 next[j-1]继续匹配，直到无路可退（即退到 0）。为了使代码更加好写，这里通常将 j∈[0,lenp−1]j \in \rm [0, len_p-1]，而母串 ss 中是 i∈[1,lens]i \in \rm [1, len_s]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+10;
char p[N], s[N];
int ne[N];

int main() {
  scanf("%s%s", p+1, s+1);
  int lp = strlen(p+1);
  int ls = strlen(s+1);

  // 求 next
	
  for (int i = 1, j = 0; i <= ls; i++) {
      while (j != 0 && s[i] != p[j+1]) j = ne[j];
      if (s[i] == p[j+1]) j++;
      if (j == lp) {
          printf("%d ", i-j);
          j = ne[j];
      }
  }
}

注意我们这里的下标都是从 1 开始的，这样可以省去很多不必要的麻烦。

总结这三个步骤：

  1. 检测是否能够回退 j 并且回退直到无法回退，包含 j 已退到开头和当前位置匹配成功两种情况。
  2. 如果当前位置（i 与 j+1）匹配成功，将 j 后移一位。
  3. 检测是否匹配结束，并且将 j 回退一次接着匹配下一个。

next 数组

构造 next 数组的过程就是一个匹配的过程，所以大体代码与上文类似。

1
2
3
4
5
6
ne[1] = 0;
for (int i = 2, j = 0; i <= lp; i++) {
    while (j != 0 && p[i] != p[j+1]) j = ne[j];
    if (p[i] == p[j+1]) j++;
    ne[i] = j;
}

注意，这里一定要从 2 开始循环，因为 j 为 0 时如果从 1 开始就会导致 p[i] == p[j+1]，从而构建错误的 next 数组。其次，next[1] = 0 是一定的。

用两张图来演示这一过程，首先是第一次匹配时：

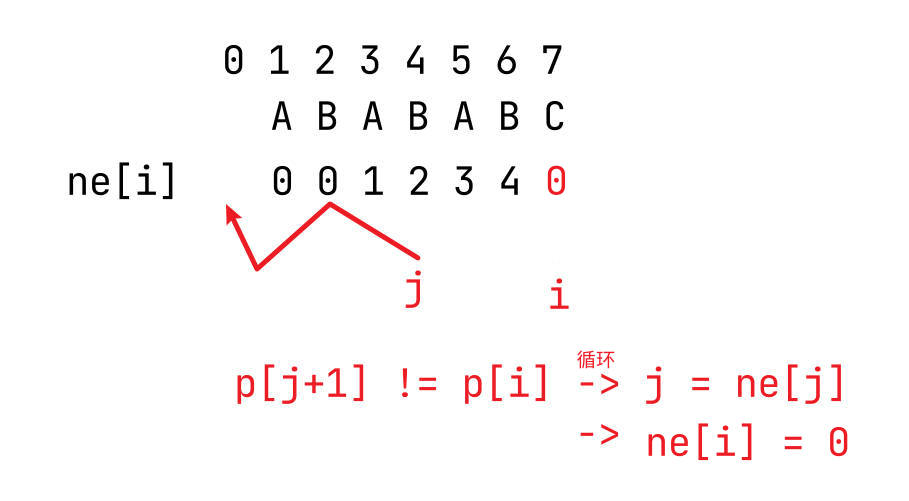
其次是匹配失败时回退的情况：

小结

KMP 算法通过将相同前缀后缀的长度储存到 next 数组中来避免匹配时重复操作，将 O(n2)O(n^2) 的暴力算法优化到了 O(n)O(n) 复杂度。